백준 17611: 직각다각형
이번에 푼 문제는
https://www.acmicpc.net/problem/17611
17611: 직각다각형이다. 이번 포스트는 다른 글과 다르게 두 가지 풀이법을 제시할 것이다.
처음에 내가 떠올린 것은 "스위핑"방법이다.
input은 시계 방향으로 제시되니, 인접한 두 개의 점을 하나의 선분으로 바꿀 수 있다.
자세히 말하면, X축에 평행한 선분들과 Y축에 평행한 선분으로 나누고, 만약 Y값이 같으면 X축 선분에, X값이 같으면 Y축 선분에 평행한 그룹에 추가하는 방식이다.
이제 스위핑을 할 것인데, 일단 선분 집합을 Sort한다. 이러면 가장 왼쪽에 있는 선분을 먼저 들여다 볼 수 있다. 그 다음 선분을 순회할 것인데, 여기서 나는 최소 우선순위 큐를 사용했다. 이 우선 순위 큐는 지금까지 순회했던 선분의 오른쪽 점을 저장해서, 만약 현재 선분의 왼쪽 점보다 작으면 pop을 한다. 이미 Sort를 하였기 때문에, 현재의 선분은 이전의 선분보다 왼쪽에 있다는 것이 확정이 되어있다. 그래서 오른쪽만 확인해서, 현재의 선분과 겹치지 않는 선분들의 제함으로써, 우선순위 큐의 사이즈로 현재의 선분과 겹치는 선분의 갯수를 구할 수 있다.
그렇게 나온 코드는 다음과 같다. 나는 우선순위 큐에서, 가장 작은 값을 구하기 위해서 값에 마이너스를 붙였다.
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
vector<pair<int, int>> input, H, W;
int N, X, Y;
int solve(vector<pair<int, int>>& pos)
{
sort(pos.begin(), pos.end());
priority_queue<int> pq;
int ret = 0;
for (int i = 0; i < pos.size(); i++)
{
int a = pos[i].first;
int b = pos[i].second;
while (!pq.empty() && -pq.top() <= a) pq.pop();
pq.push(-b);
ret = max(ret, (int)pq.size());
}
return ret;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N;
for (int i = 0; i < N; i++)
{
cin >> X >> Y;
input.push_back({ X, Y });
}
input.push_back(input[0]);
for (int i = 0; i < N; i++)
{
if (input[i].first == input[i + 1].first)
{
int a = input[i].second;
int b = input[i + 1].second;
if (a > b) swap(a, b);
H.push_back({ a, b });
}
if (input[i].second == input[i + 1].second)
{
int a = input[i].first;
int b = input[i + 1].first;
if (a > b) swap(a, b);
W.push_back({ a, b });
}
}
cout << max(solve(H), solve(W)) << '\n';
}안타깝게도 이 코드는 "틀렸습니다"를 받았다. 이유는 무엇일까? 하지만, 나는 그 이유를 고민하기 귀찮아서, 이 문제의 해결을 미뤘다. 그렇게 시간이 흐르고, 나는 이 문제와 다시 마주하기로 결심한다. 이전에 제출했던 코드를 분석해서, 어떻게 해결방법을 모색했고, 문제점이 무엇인지 고민해볼려고 했다.
그런데, 문제를 다시보니, 다른 해결책이 떠올랐다. 왜 지금와서 다른 해결책이 떠올랐냐면
https://www.acmicpc.net/problem/19951
본문의 문제 해결을 미룬 사이에 푼 이 문제 덕분이다.
이 문제는 구글링을 통해 해결했는데, 내가 누적합 문제를 다시 볼 수 있게 도와준 좋은 문제였다. 간단히 설명하면, 가장 왼쪽에 위치한 값에 +를 하고, 가장 오른쪽에 위치한 값에 -를 해서 누적합을 통해 정답을 빠르게 구할 수 있다.
참조: https://yabmoons.tistory.com/729
[ 백준 19951 ] 태상이의 훈련소 생활 (C++)
백준의 태상이의 훈련소 생활(19951) 문제이다. [ 문제풀이 ] 매우 간단하게 풀 수도 있는 문제이지만, 자칫하면 시간초과에 걸릴 수 있는 문제이다. 간단하게 풀었을 때의 문제점과 이를 해결하기
yabmoons.tistory.com
입력값으로 주어진 x, y의 값은 -500,000이상, 500,000 이하이다. 그렇다면, 똑같이 input을 가공해서 선분을 만들고, 1,000,000 가량의 사이즈를 갖는 배열을 준비한 뒤, 선분의 왼쪽 값을 +하고, 오른쪽 값에 -를 한 뒤에, 순회를 하면 누적합을 구해서, 가장 큰 값을 구하는 아이디어를 떠올렸다. 원래의 값에 500,000을 더해서 음수를 방지를 하는 것도 잊지말자.
그렇게 나온 코드는 다음과 같다.
#include <iostream>
#include <vector>
using namespace std;
const int MAX = 500000;
vector<pair<int, int>> input, H, W;
int N, X, Y, cx[2 * MAX + 3], cy[2 * MAX + 3], sx = 0, sy = 0, ans = 0;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N;
for (int i = 0; i < N; i++)
{
cin >> X >> Y;
input.push_back({ X, Y });
}
for (int i = 0; i < N - 1; i++)
{
if (input[i].first == input[i + 1].first)
{
int a = input[i].second;
int b = input[i + 1].second;
if (a > b) swap(a, b);
cx[a + MAX]++;
cx[b + MAX]--;
}
if (input[i].second == input[i + 1].second)
{
int a = input[i].first;
int b = input[i + 1].first;
if (a > b) swap(a, b);
cy[a + MAX]++;
cy[b + MAX]--;
}
}
for (int i = 0; i < 2 * MAX + 3; i++)
{
sx += cx[i];
sy += cy[i];
ans = max(sx, ans);
ans = max(sy, ans);
}
cout << ans << '\n';
}이제 정말 정답일까? 안타깝게도 아니다... 도대체 무엇이 문제일까? 분명 두 아이디어에 틀린 부분이 있다고 생각이 전혀 들지 않는데, "틀렸습니다"란 결과가 나오니, 나한테 자신이 없어졌었다. 결국 나는 여러 시도를 했는데 문제 지문에
단, 수평선 H는 다각형의 어떤 수평선분과도 겹처 놓여서는 안 되고, 유사하게 수직선 V는 다각형의 어떤 수직선분과도 겹쳐 놓여서는 안 된다.
이것을 보고, 점이 위치한 선분을 제외하는 것을 고려했고, 시도도 했었다. 하지만, 문제의 예제 2도 통과하지 못했다.
나는 왜 이 아이디어가 예제 2를 통과 못하는 지 궁금해져서 예제 2를 그림판으로 그림을 그렸었다.
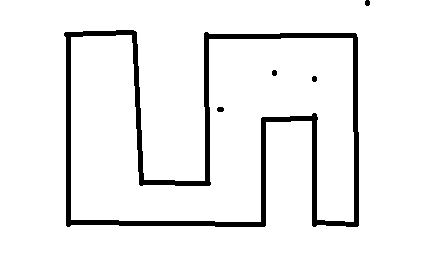
그림을 그리고 나서야, "아.. 수직 / 수평 선분이 정수란 보장이 안되어있어서, 애꿎은 값만 건너뛰기 때문에 답이 전혀 아니구나.."라고 알게 된 동시에, 나는 지금까지 엄청난 실수를 했다는 것을 깨달았다. 내가 그림을 그릴 때, 선분 하나가 비어서 이상하다 여겼었는데, 이 문제의 다각형은 시계방향으로 진행하다가, 시작점으로 되돌아온다는 것을 이제야 알게 되었다. 즉, 나는 마지막 점이 시작 점으로 되돌아오는 선분을 고려하지 않은 것이다. 결국 나는 두 아이디어를 수정해서 다시 제출했다.
// 누적 합 방식
#include <iostream>
#include <vector>
using namespace std;
const int MAX = 500000;
vector<pair<int, int>> input;
int N, X, Y, cx[2 * MAX + 3], cy[2 * MAX + 3], sx = 0, sy = 0, ans = 0;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N;
for (int i = 0; i < N; i++)
{
cin >> X >> Y;
input.push_back({ X, Y });
}
input.push_back(input[0]); // 추가
for (int i = 0; i < N; i++)
{
if (input[i].first == input[i + 1].first)
{
int a = input[i].second;
int b = input[i + 1].second;
if (a > b) swap(a, b);
cx[a + MAX]++;
cx[b + MAX]--;
}
if (input[i].second == input[i + 1].second)
{
int a = input[i].first;
int b = input[i + 1].first;
if (a > b) swap(a, b);
cy[a + MAX]++;
cy[b + MAX]--;
}
}
for (int i = 0; i < 2 * MAX + 3; i++)
{
sx += cx[i];
sy += cy[i];
ans = max(sx, ans);
ans = max(sy, ans);
}
cout << ans << '\n';
}// 스위핑 방식
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
vector<pair<int, int>> input, H, W;
int N, X, Y;
int solve(vector<pair<int, int>>& pos)
{
sort(pos.begin(), pos.end());
priority_queue<int> pq;
int ret = 0;
for (int i = 0; i < pos.size(); i++)
{
int a = pos[i].first;
int b = pos[i].second;
while (!pq.empty() && -pq.top() <= a) pq.pop();
pq.push(-b);
ret = max(ret, (int)pq.size());
}
return ret;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N;
for (int i = 0; i < N; i++)
{
cin >> X >> Y;
input.push_back({ X, Y });
}
input.push_back(input[0]); // 추가
for (int i = 0; i < N; i++)
{
if (input[i].first == input[i + 1].first)
{
int a = input[i].second;
int b = input[i + 1].second;
if (a > b) swap(a, b);
H.push_back({ a, b });
}
if (input[i].second == input[i + 1].second)
{
int a = input[i].first;
int b = input[i + 1].first;
if (a > b) swap(a, b);
W.push_back({ a, b });
}
}
cout << max(solve(H), solve(W)) << '\n';
}
이제야 정답을 얻었다.. 결국 답은 바로 곁에 있었는데, 머나먼 길을 돌아왔다.. 비록 나중에 생각한 누적합이 메모리를 많이 더 차지하지만, 문제를 풀며 실력이 늘었다는 것을 느끼게 된 좋은 시간이 되었다.