백준 15791: 세진이의 미팅

https://www.acmicpc.net/problem/15791

 

 

이 문제와 비슷한 문제인

https://www.acmicpc.net/problem/11401

 

백준 11401: 이항 계수 3는 예전에 해결한 적이 있다. 하지만, 사용된 페르마의 소정리를 완전히 이해하지 않고 넘어갔고, 관련 문제도 안 푼지 오래되어서 오랜만에 관련 개념도 정리하고, 문제도 해결을 해보려한다.

 

일단 문제 읽고나면 이항 계수를 사용해야한다는 건 그리 어렵지 않게 알수 있다. 왜냐하면 남학생 n명 중에 미팅을 해야할 m명을 골라야하니, 정답은 nCm (mod 1000000007)이란건 금방 알 수 있다.

 

문제는 n의 값이 최대 1,000,000이라서 내가 이전까지 알던 DP 방식으로는 O(N ^ 2)의 복잡도를 가지기에 이 문제를 해결하기 좋은 방식이 아니다. 그러면 어떻게 해결을 해야할까? 이것을 위해 페르마의 소정리에 대한 개념을 이해하고 넘어가려한다.

 

페르마의 소정리는 다음과 같다.

출처: https://namu.wiki/w/%ED%8E%98%EB%A5%B4%EB%A7%88%EC%9D%98%20%EC%86%8C%EC%A0%95%EB%A6%AC

증명은 다음과 같다. a는 p의 배수가 아니고, p는 소수라한다.

 

1) A = {1, 2, 3, .. , p - 1}과 A에 각각의 원소에 a를 곱한 B = {a, 2 * a, 3 * a, ... (p - 1) * a}가 있다고 한다.

 

2) B의 각각의 원소에 p로 나눈 나머지로 만든 집합은 A와 동일하다.

2의 증명)

- p보다 작은 서로 다른 자연수 m과 n이 있고(0 < n < m < p), m * a와 n * a의 p의 나머지는 R이란 동일한 수가 존재한다고 가정을 하자 이를 식으로 나타내면 다음과 같다,.

 

m * a = p * D1 + R

n * a = p * D2 + R

이 두 식을 빼면

a(m - n) = p * (D1 - D2)

이렇게 나타낼 수 있다.

즉, a * (m - n)는 p의 배수이다. 그런데 a는 p의 배수가 아니라고 처음부터 가정을 하였고, (m - n)은 p보다 작기 때문에 p에 대해 서로 다른 나머지를 가지는 m * a와 n * a는 존재하지 않는다는 것이 증명되었다.

 

3) A의 원소들을 전부 곱한 후의 p로 나머지를 구한 값은 B의 원소들을 전부 곱한 후의 p로 나머지를 구한 값과 동일하다.

즉, 

(p - 1)! * (a ^{p - 1})  ≡ (p - 1)! (mod p)이다.

양변의 (p - 1)!을 나누면

 

a ^{p - 1} ≡ 1 (mod p)

란 식이 나온다. 각각에 a를 곱하면.

 

a ^p ≡ a (mod p)

이런 식이 완성된다. 이렇게 페르마의 소정리를 증명하였다.

 

이렇게 먼 길을 돌아왔는데, 그럼 이걸 어떻게 활용해야 문제를 해결을 할 수 있을까?

이 페르마의 소정리의 식을 약간 변형 시키면, 다음과 같이 쓸 수 있다.

 

a ^{p - 2} ≡ a^-1 (mod p)

즉, 답이 보이지 않던 분수의 나머지를  a ^{p - 2} 만큼 곱하면 나머지를 구할 수 잇다면 결론이 나온다.

이항 계수의 식은 다음과 같다.

출처: https://m.blog.naver.com/hongjg3229/221650178981

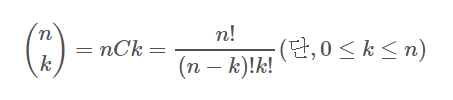
그렇다면 이 식을 소수인 P = 1000000007의 나머지를 구한다면 다음과 같은 식으로 변형할 수 있다.

((n! % P) * (((n - k)!k!)^{P - 2} % P)) % P 

 

여기서 거듭제곱은 이전에 다루었던 분할 정복 방법을 사용하면 된다.(https://sumserv.tistory.com/92)

이제 코드를 구성하면 다음과 같이 사용할 수 있다.

#include <iostream>

using namespace std;
using ll = long long;
const ll MOD = 1000000007;
ll N, M, L = 1, R = 1;

ll pow(ll n, ll cnt)
{
	if (cnt == 0) return 1;
	if (cnt % 2 > 0) return (pow(n, cnt - 1) * n) % MOD;
	ll h = pow(n, cnt / 2);
	return h * h % MOD;
}
int main()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);
	cin >> N >> M;
	for (int i = 2; i <= N; i++)
		L = (L * i) % MOD;
	for (int i = 2; i <= M; i++)
		R = (R * i) % MOD;
	for (int i = 2; i <= N - M; i++)
		R = (R * i) % MOD;
	cout << L * pow(R, MOD - 2) % MOD << '\n';
}

 

이 문제를 풀기 위해서 사이트를 돌아다니고, 블로그로 글을 정리하며 드디어 이해하기 힘들었던 페르마의 소정리를 이해할 수 있게 되어서 속이 시원하다. 다음에도 이해하기 힘든 개념이 있으면 글로 정리해보자.

 

참조:

https://m.blog.naver.com/hongjg3229/221650178981

[백준 11401] 이항 계수3 - 페르마의 소정리, modular inverse

https://blog.naver.com/a4gkyum/220768006509

페르마의 소정리 (내용과 증명)

https://ko.wikipedia.org/wiki/%ED%8E%98%EB%A5%B4%EB%A7%88%EC%9D%98_%EC%86%8C%EC%A0%95%EB%A6%AC

페르마의 소정리 - 위키백과, 우리 모두의 백과사전